Mon, 19 Sep 2011
僕が2002年にIDM(注:IDMは語の再帰的な伝播量を語の影響力とする問題に対するアルゴリズムの名称です)を考えたときは、対象となるデータセットが小規模だったので計算量のことなんて何も考えてませんでした。しかし最近では、計算機のメモリにのらないような大規模なデータを効率よく分析する必要も出てきたので、そうも言ってられなくなってきました。例えばホットリンクが提供している東日本大震災に関連するツイートデータは約2億1千万ツイートもあり、従来のナイーブなIDMのアプローチで分析することは不可能でした。
最近のトレンドからすると大規模なデータにはHadoopで、ということになるのかもしれませんが、僕の典型的な文系研究室にはMacBook Air (Early 2010) とiMac (Late 2009) と7年前のWindows XPマシンしかないし、分散処理は基本的には台数効果しかなさそうなので本質的な解決策にはなりません。
データが増えれば多少の誤差は気にしなくてもいいでしょう、ということで、近似解でもいいのでIDMのアルゴリズムの高速化・省メモリ化を考えていました。先日書いたビットストリームによる類似文書の検索もその一つなのですが、この方法だと
- 新しい文書が追加されたときに差分だけ計算することができない
- 文書や投稿者のIDM影響力は求めることができても語の影響力を求めることができない
のでイマイチやなあと思っていました。
そこで次なる手として、ランダムネットワークを想定したときのIDM影響力の期待値を以前求めていたので、ランダムネットワークを実際のネットワーク構造を反映させたものに置き換えることでIDM影響量を確率的に求めることを思いつきました。
具体的には、どの語がどの文書に登場するかが分かり、文書ごとにどれくらい拡散する力をもっているかが分かればいいのですが、前者は転置インデックスから求まり、後者は隣接行列から確率的に求まります。
語wを含む文書集合をDw、語wの頻度をfw、全文書数をN、隣接行列Mのノイマン級数における文書dの出次数の和をl_dとすると、語wのIDM影響力I(w)は
Iw=fw (fw -1) / (N(N-1)) ¥sum_{d ¥in Dw} ¥sum_i^n l_d ... (1)
で求まります。以降ではこの手法をIDMstatと呼ぶことにします。
また、同じノード数N、リンク数L、語の出現頻度fwにおける語wのIDM影響力の期待値Ewは、
Ew=(fw-1) R / (1 - ¥beta R)、R=L fw /(N(N-1)) ... (2)
で求まりますので、Iw/Ewの大きな語wが特徴的な語ということになります。
この方法で本当に処理速度が早くなっているかを確認するために、手元の小さなデータセット(文書数5890、リンク数1890、語の種類数649)を使って検証してみました。100回計算したときの処理時間を測ったところ、IDM(従来の行列計算による方法)では0.317秒かかったのに対して、IDMstatでは0.071秒でした。このデータセットだと4.5倍程度速くなっているだけですが、IDMstatだとデータ数に対して線形にしか計算量が増えないし、保持するデータ量も少なくて済むので、データ数が増えればもっと顕著な差が出てくると思います。
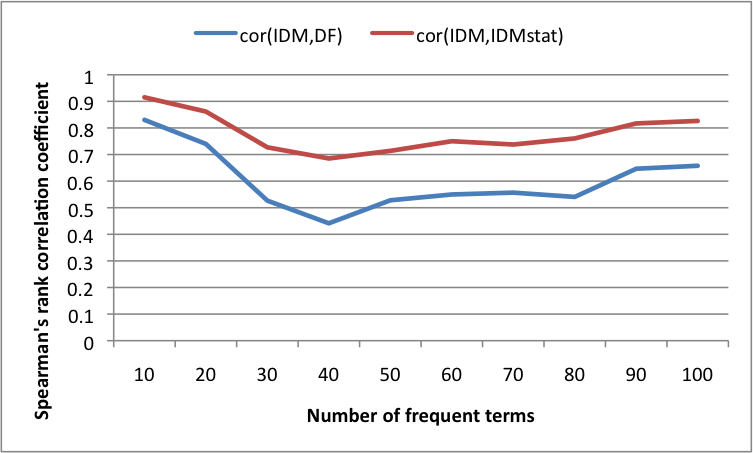
また、IDMでは厳密解が得られるので、その結果をgold standardとしたときのIDMstat精度評価をしてみました。頻度(出現頻度ではなくて文書頻度)が高いほど影響力も高くなる(ので実際に使うときは影響量の期待値で割って正規化する)ので、IDMと文書頻度DFとIDMstatの結果の順位相関係数を出してみました。結果を下図に載せていますが、期待通りIDMstatはDFよりもIDMに近い結果になりました。
ここで提案したIDMstatはデータ全体における語のIDM影響力しか分かりませんが、式(1)におけるDwを変えることで文書毎や投稿者毎の語のIDM影響力も同じように分かります。また、新しい文書が追加されたときに差分だけ計算することができるので、大規模データにも使えそうな気がしています。
今後はIDMstatを東日本大震災に関連するツイートデータに適用してみて本当に使えるか検証してみようと思っていますが、そろそろ違うことがしたくなってきたので、いつになるかは分かりません。。。
返信関係などで構造化されたテキストデータ(例えばブログやツイッターなど)から影響量を求める拙作IDMは基本的に再帰構造行列と類似度行列のシュア積で求まるのですが、大規模データに適用するときは後者の計算量がO(kn^2)(kは特徴数、nはテキストデータ数)なのがネックになっていました。(ちなみに、前者は疎行列なので、平均出リンク数をmとするとO(nm)で求まります)
そんな折、ツイッター上で@junkimaruiくんからLSHを使えばできることを教えてもらったのでいろいろ調べてみました。LSHはハッシュ関数をかまして長いテキストベクトルを短いビットストリームにしたうえでビットソートするところが肝です。
LSHを知らなかった僕には目からウロコの素晴らしい手法で、これまで知らなかったことを恥じつつIDMに適用できないかなーと考えていたのですが、ハッシュ関数をかますときにテキストベクトルの特徴数を限定するし、ハッシュ関数をかますことで確率的に誤差を埋めこんでしまいます。
最初は再帰構造行列をハッシュ関数として表現できないかなーとか無茶なことを考えていたのですが、ふと、テキストベクトルを0-1バイナリで作成してシャッフルしつつビットソートしても似ているベクトルは近くに来る確率は高いので、ハッシュ関数をかまさなくてもできるような気がしてきました。
ということで、実際にプログラムを書いて実験してみました(プログラムは http://www.friendpaste.com/6mww7pmKudClo2HbGQtEso で公開しています)。
その結果、特徴数100、ビット充填率=0.2〜0.6、ビーム幅10、permutation10回において、
- テキスト数500のとき、全探索15.8秒、ビットストリーム検索12.9秒
- テキスト数1000のとき、全探索59.9秒、ビットストリーム検索24.9秒
- テキスト数10000のとき、全探索5915秒、ビットストリーム検索248秒
となり、ビットストリーム検索はデータ数に対して線形時間で処理できることが分かりました。
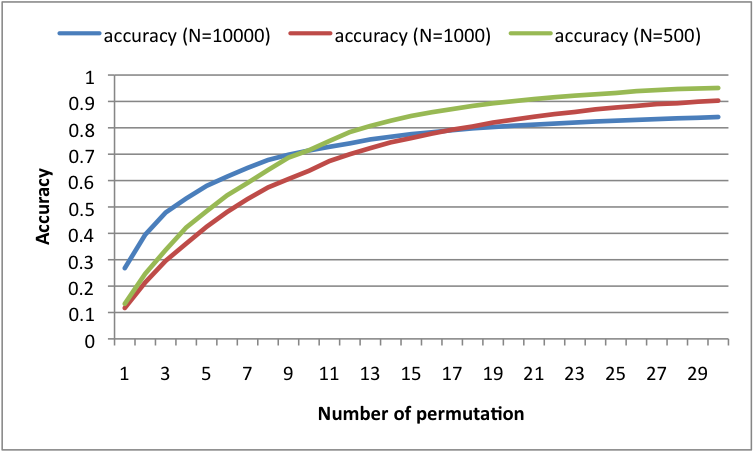
また、全探索をした結果をgold standardとしたときのビットストリーム検索の精度は以下の図ようになりました。横軸はpermutation(ビットのシャッフル)の回数、縦軸は精度です。permutation10回で精度0.7くらい、permutation30回で精度0.9くらいなので、そこそこ精度が出ています。
とまあここまでやってから調べてみたら、上記のような方法はApproximate Nearest Neighborの分野で古くから研究されつくされている方法でした。そりゃそうですね。テキストデータのように素性が数万もある場合はやはりLSHのような方法で短いビットストリームにしたほうが処理速度は確実に早くなりますが、素性数を限定するんならビットストリーム検索でも十分かなと思いました。
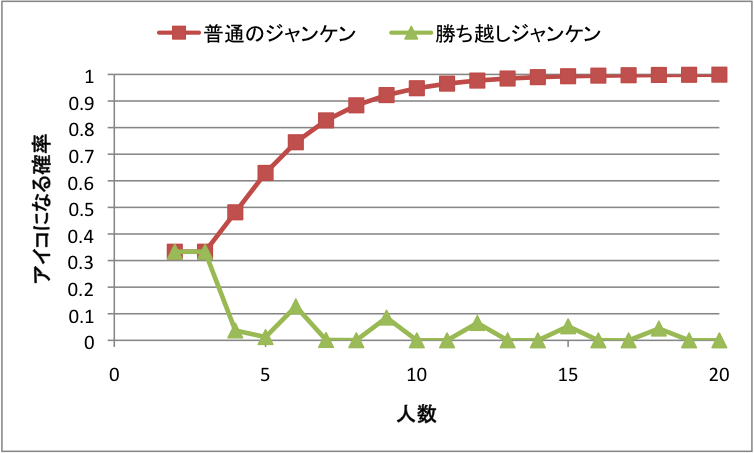
娘たちとジャンケンをしているとアイコが多いので「勝ち越しジャンケン」というのを思いついた。例えば4人でジャンケンしてグー・チョキ・パー・パーだったとすると、チョキの人のみ勝ち越してるから勝ち。勝ち越しジャンケンだと、アイコになる確率がかなり下がる。
アイコになる確率は、普通のジャンケンだと1-(2^n-2)/3^(n-1)。勝ち越しジャンケンだと3/3^n (nが3の倍数でないとき)、(3+C(n,n/3)*C(n/3*2,n/3))/3^n (nが3の倍数のとき)。
アイコになる確率をExcelで計算した結果は下図。勝ち越しジャンケンの方が圧倒的に低い。
ジャンケンの人数が多くなると、よく「多いもん勝ち」「少ないもん勝ち」という変なルールが導入されるけど、これは「グーがチョキに勝ち、チョキがパーに勝ち、パーがグーに勝つ」というジャンケンのルールを無視しているので気持ち悪い。
一方、勝ち越しジャンケンはジャンケンのルールを拡張したものと見なすことができる。また見方を変えれば、2部グラフによって勝敗を決める従来のジャンケンに対し、重みつき有向グラフによって勝敗を決めるのが勝ち越しジャンケンといえる(かもしれない)。
重み付き有向グラフで考えるといろんな拡張ができる。1人あたり討ち取り数のような評価関数や、強い相手を倒した方がよりポイントが大きいPageRank的な評価関数も実現可能(頭の中で計算するのは無理ですが)。
いずれにせよ重要なのは、ジャンケンにおいて「グーがチョキに勝ち、チョキがパーに勝ち、パーがグーに勝つ」という大原則に従って、様々な拡張が可能であるという点。大原則さえ守られていれば、評価関数の些細な違いは気にならない。
ただ、勝ち越しジャンケンだと、他の人の手を全て見ないといけないので、人数が多くなったら実現はほぼ不可能。というわけで、人数が多くなったら適当にグループに分かれて普通にジャンケンするのが一番いいかも。